Red-Black Tree(RB Tree)を書いてみた
リンク切れをなおした
Goで赤黒木を書いた。 赤黒木は平衡二分探索木の一種で順序つき辞書として利用できる。 Linux kernel 2.6.23以降ではタスクスケジューラーでも利用されているらしい。
効率は比較的よく、挿入・削除・検索の各操作の最悪時間計算量は全て O(log(n)) となる(n は要素数)。
今回は辞書として使えるように Lookup(),Insert(),Delete() の3つを実装した。 また実装は短命で永続データ構造には出来ていない。
リバランスの詳細はここを参考にした。 ただ、実装にあたり選択肢が幾つかあったし悩んだのでメモする。
実装上で悩んだところや反省
- ノード間の接続をどのように扱うか?
- ツリーはノードか?
- ツリーの更新操作をどのように実装するか?
- リーフノードをどうするか?
- リバランス処理の起点がどこかわからない
ノード間の接続をどのように扱うか?
ノード間の接続は双方向に参照を持たせることにした。2つ理由があった。
1つめは挿入・削除後の平衡を保つ処理がルートに向かいながら実施るように定義されていたため。 そのまま葉から根へ再帰するような実装を考えていた。
2つめは片方リンクにして再帰関数を使うとコールスタックが木の深さに依存するのが嫌だと感じたため。 ただ再帰をスタックで書き直せば解消すると考え直している。
(そもそも平衡が保たれるので木の深さも最悪時で O(log(n)) となり大きな問題にならない)
双方向リンクを使って実装することにしたため、ルートノードをどうするか判断することになった。 ここでは親へのリンクに自分への参照を持たせることにした。
ツリーはノードか?
双方向リンクを使ったためにルートノードが特別な性質(自分への参照を持つ)を持つことになったため、ツリーとノード構造体を明示的に分けることにした。
ツリーの更新操作をどのように実装するか?
初めての実装ではノード(*Node)への参照を使って直接書き換えていた。 参照の付け替えが多く、回転操作の実装を考えるのが煩雑になった。
そこで2回目の実装では回転後のノードを返す関数を準備した。 呼び出し元でノードを接続するようにした。 しかし、呼び出し元で正しい繋げ方を保持する必要があり、特に削除で非常に煩雑になった。
そこで2回目の実装では途中で方針を変えた。書き換え先を表すplaceという構造体を準備した。 このplaceがルートノード,左ノード,右ノードの書き換えや双方向リンクの保持などを隠蔽する。 同時に、更新操作が副作用を保つようにして回転後には既に親ノードと整合しているようにした。
結局、ちゃんとテストを書いて煩雑な処理を隠蔽できる適切な範囲を切り出すのが大事だった。
リーフノードをどうするか?
nil にした。リーフノードの領域を確保するのが嫌だったため。
リバランス処理の起点がどこかわからない
問題は2つ。リバランスを行う関数に渡すの引数をどのようにするか? そもそも削除の際にリバランスを行うべき箇所はどこなのか?
挿入時
挿入後のリバランスは挿入されたノードを引数に取ることにした。
主な理由は挿入後のリバランスで新規ノードを起点に親方向に探索したパターンマッチで分岐が決まるため。 親や祖父ノードをわたす事にするとリバランスの関数にマッチパターンを値として渡さないとならず冗長になると考えたから。
削除時
削除後のリバランスでは削除されたノードの親と子の位置を引数に取ることにした。 削除された箇所(子ノード)が nil となる場合がありこうなった。 また分岐は削除ノードの兄弟ノードが関わるため親ノードと親ノードから削除済みノードの場所を渡すのは自然に思えた。
赤黒木の削除時にリバランスが必要になるのは黒ノードが削除された時のみだが、 平衡木でのノード削除は別ノードから値を上書きするなどの操作が起きるため何が削除されたとしていいか最初わからなかった。
そこで削除の際に起点となるノードや削除された色については自分で判断した。 削除の起点には大きく4パターンある。
- 削除するノードが子ノードを持たない(case-0): 削除対象のノードを起点とする
- 削除するノードが子ノードを持つ:
- 左ノードがなく、右ノード(del.r)がいる(case-1): del.r で置き換え起点とする
- 左ノードがいる: 左ノードを含めた子孫の最大値のノードで置き換える
- 代替ノード(src)が左ノードを持たない(case-2): src を起点とする
- 代替ノード(src)が左ノード(src.l)を持つ(case-3): src.l を起点とする
ここに各ケースでのノードの移動とリバランスの起点について図を置いておく。
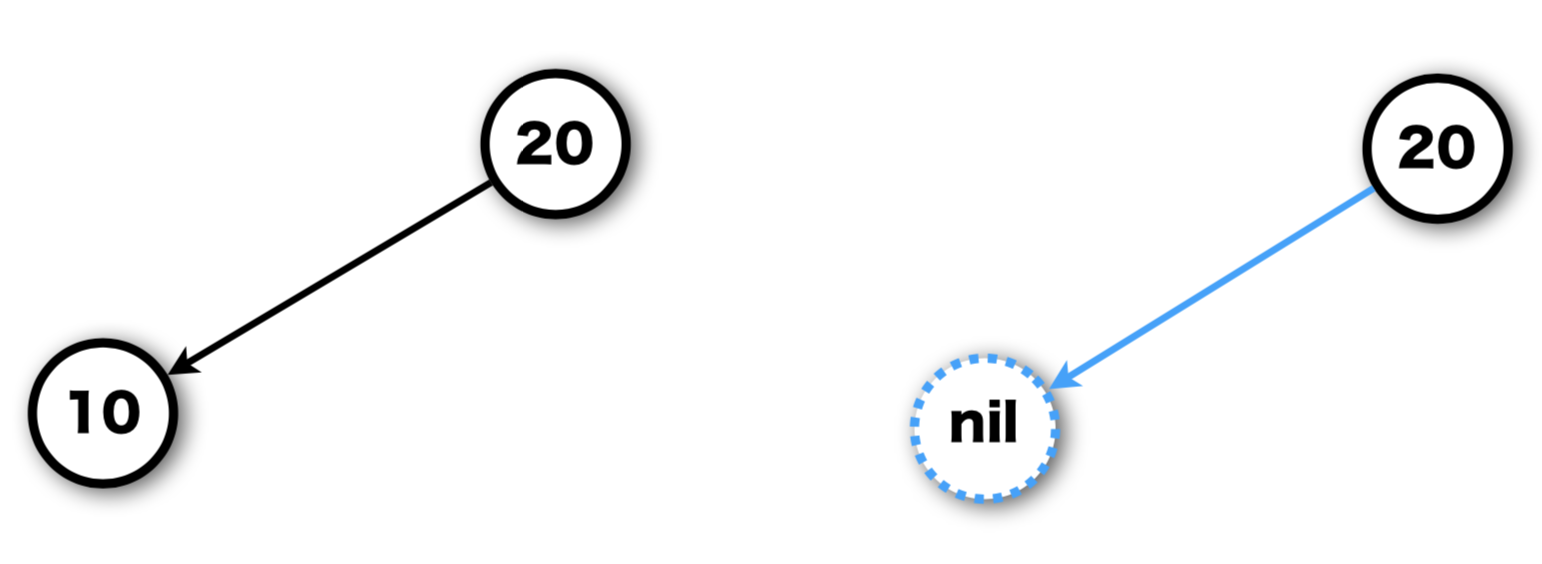 Case 0
Case 0
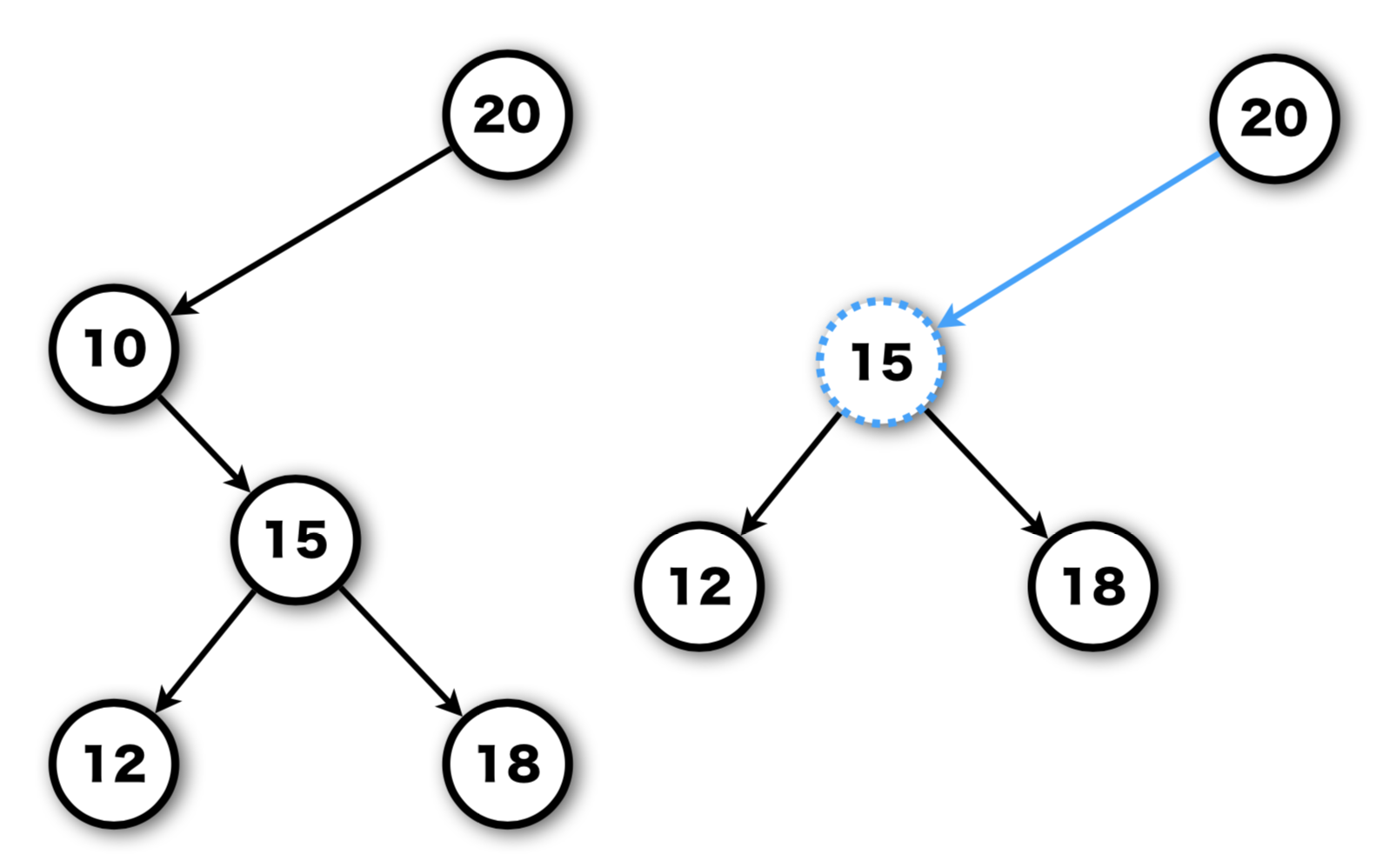 Case 1
Case 1
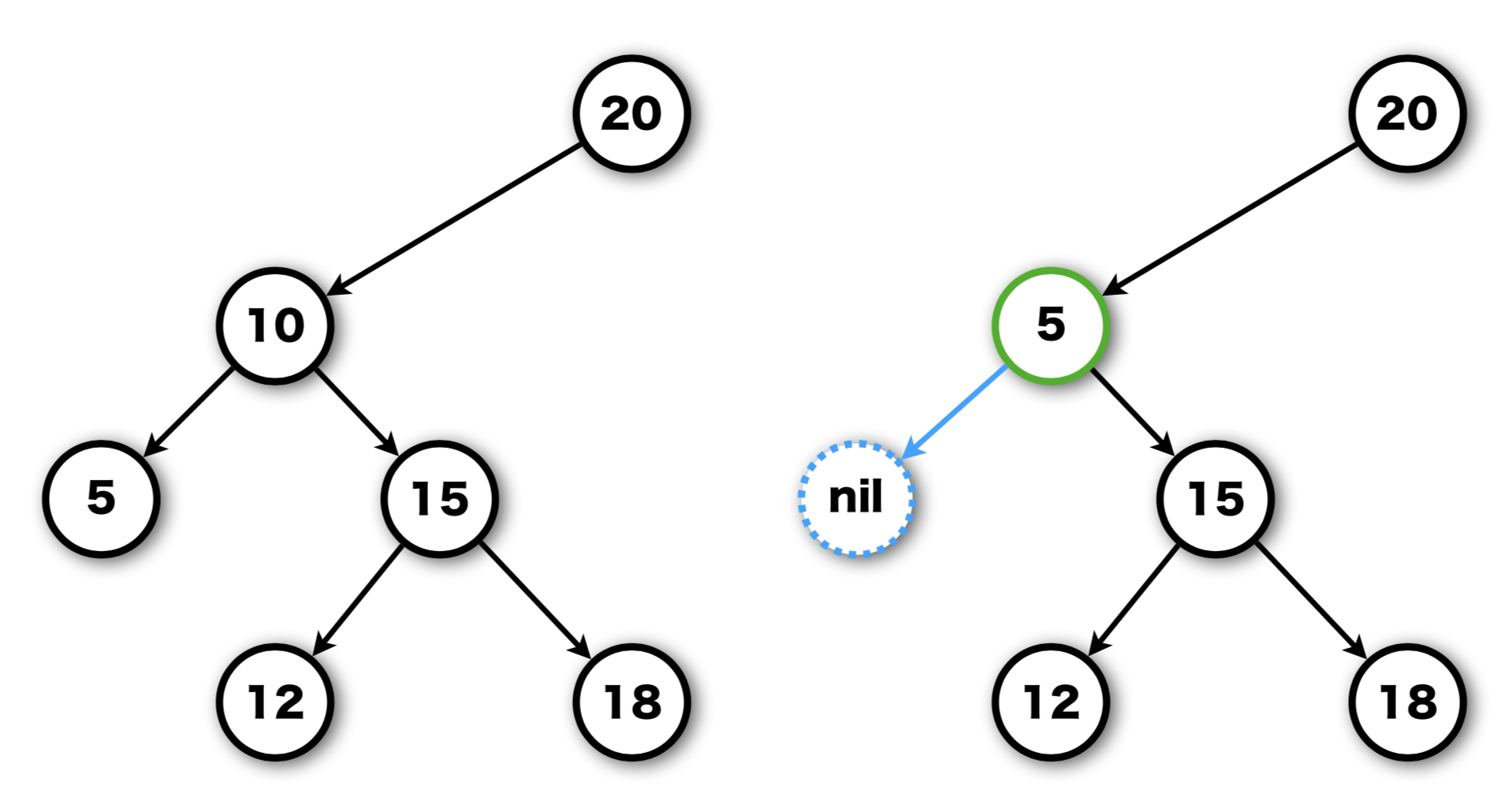 Case 2.0
Case 2.0
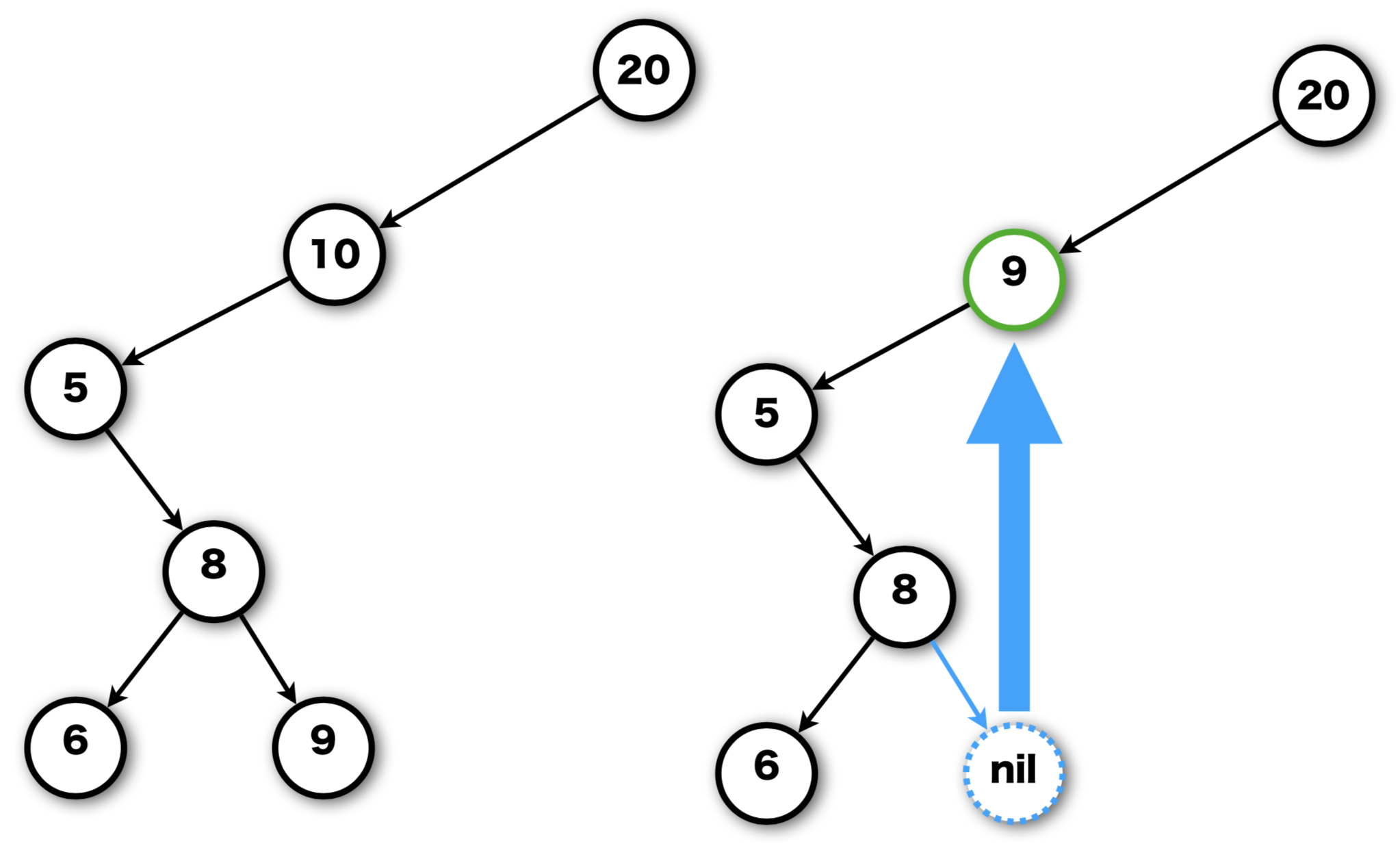 Case 2.1
Case 2.1
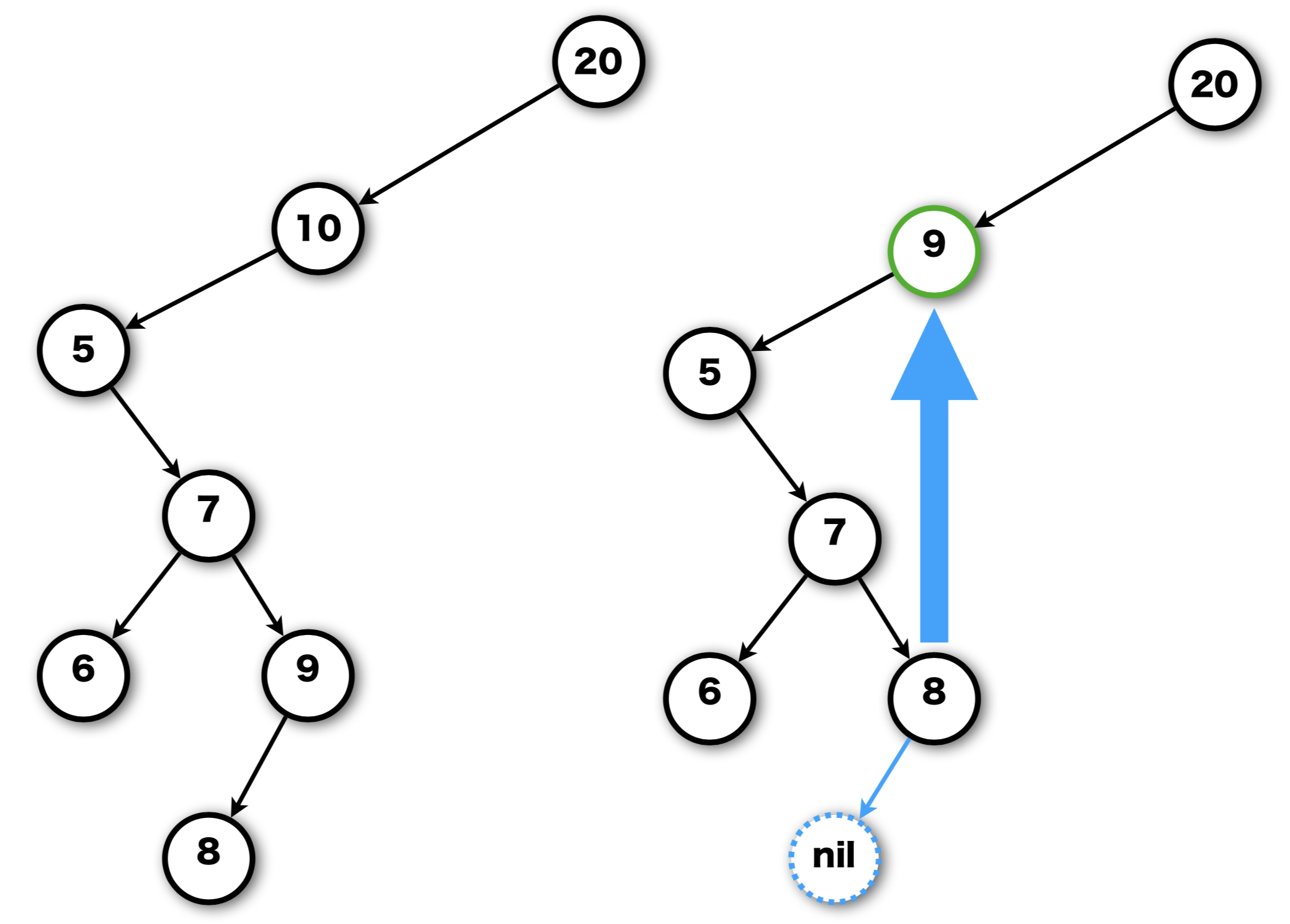 Case 3
Case 3
このように削除は代替ノードに差し替えにより実現される(Case-1,2,3)。
そして削除対象のノードが代替ノードで置き換わる際に値はコピーされるが色は変わらない。 たとえばCase-3の場合、はじめ 10 のノードが赤で 9 ノードが黒の場合、差し替え後の 9 ノードは赤になる。
図の点線のノードがリバランスのスタート地点になる。そして起点となるノード(点線ノード)の元の色が削除された色となる。
Case-1はわかりにくいので補足する。 差し替え後の 15 番ノードは差し替え前の 10 番ノードと同じ色になる。 削除された色は差し替え前の 15 番ノードの色になる。
ツリーとして失われた色とその場所が問題になる。
反省
- 1回目の実装ではテストが少なかった
- ノードやサブツリーとしての同値性を定義しないまま実装したら混乱した
- 配列,片方リンク,双方向リンクをデータ構造の基本単位として意識していなかった
- データ構造の永続性を事前に意識して選べないままに実装していた
- テーブル駆動でテストを書いたけど t.Run() を最初から積極的に使うべきだった
- stretchr/testifyを使って遊んでみればよかった
- 探索時の最適化( O(2log(n)) -> O(log(n)+1) )をすればよかった